The Completeness of the Real Numbers (ℝ) and Convergence of Sequences
The completeness of the real numbers ensures that there are no “gaps” or “holes” in the number line. It plays a crucial role in understanding the convergence of sequences. Here’s how:
1. Least Upper Bound (LUB) Property
The Least Upper Bound Property states that any non-empty set of real numbers that is bounded above has a least upper bound (LUB), also known as the supremum. Similarly, any non-empty set of real numbers that is bounded below has a greatest lower bound (GLB), also known as the infimum.
This property is directly related to the convergence of sequences. If you have a monotonic increasing sequence that is bounded above, the LUB of the set of terms in the sequence is the limit to which the sequence converges. Similarly, if you have a monotonic decreasing sequence that is bounded below, the GLB of the set of terms in the sequence is the limit to which the sequence converges.
Visualizing Completeness with a Highlighter and Number Line
Imagine you have a highlighter and a number line that represents the real numbers. You can think of completeness as the ability to highlight the entire number line without missing any points.
If you were to highlight only the rational numbers, you would miss the irrational numbers, leaving “gaps” in the number line. But with the real numbers, every point on the number line corresponds to a real number, so you can highlight the entire line without missing anything.
In terms of sequences, you can think of a converging sequence as a series of points on the number line that get closer and closer to a specific value. Because of completeness, you know that this value is a real number, and there’s no “gap” where the sequence is heading.
Significance of Completeness in Convergence
The completeness property ensures that every bounded, monotonic sequence in the real numbers must converge to a real number. This is a fundamental result known as the Monotonic Sequence Theorem.
Without completeness, we could have sequences that seem to approach a limit but don’t actually converge to any real number. Completeness fills in the “gaps” and ensures that such situations don’t occur in the real numbers.
In summary, the completeness of the real numbers is essential for understanding the convergence of sequences. It guarantees that bounded, monotonic sequences have a limit in the real numbers, and it can be visualized as the ability to highlight the entire number line without missing any points. This property underpins many of the results and methods used in mathematical analysis, calculus, and beyond.
Example of Completeness for a Convergent Sequence: 1/n
Consider the sequence defined by 1/n, where n is a positive integer. This sequence converges to 0 in the real numbers. But what if 0 were not included in our number system? Let’s explore this scenario:
Sequence: 1/n
The terms of this sequence are:
- 1/1 = 1
- 1/2 = 0.5
- 1/3 ≈ 0.333
- 1/4 = 0.25
- …
Convergence to 0 in the Real Numbers
In the real numbers, the sequence 1/n converges to 0. As n gets larger, the value of 1/n gets closer and closer to 0.
Hypothetical Scenario: 0 Not Included
Now, imagine a hypothetical number system where 0 is not included. In this system, the sequence 1/n would not have a limit, because the value it’s approaching (0) does not exist in the system. The sequence would continue to get closer to a “gap” where 0 should be, but it would never actually converge.
Role of Completeness
The completeness of the real numbers ensures that every point on the number line, including 0, corresponds to a real number. This allows the sequence 1/n to converge to 0. Without completeness, and without the inclusion of 0, the sequence would not have a limit in the system.
In summary, this example illustrates how the completeness of the real numbers, including the inclusion of 0, ensures that the sequence 1/n converges to 0. Without completeness, and without 0, the sequence would not converge, highlighting the importance of completeness in understanding the behavior of sequences.
Monotonic Sequence Theorem
The Monotonic Sequence Theorem states that every bounded, monotonic sequence in the real numbers is convergent. Here’s how the proof can be understood with both rigor and intuition:
1. Definitions
A sequence is called monotonic if it is either non-decreasing (each term is greater than or equal to the previous term) or non-increasing (each term is less than or equal to the previous term). A sequence is bounded if there is a real number that is an upper bound for all the terms (for a non-decreasing sequence) or a lower bound for all the terms (for a non-increasing sequence).
2. Intuitive Understanding
Imagine a number line, and think of a monotonic sequence as a series of points on that line that are either moving steadily to the right (non-decreasing) or to the left (non-increasing). If there’s a “wall” (an upper or lower bound) that the points can’t pass, then the points must eventually get closer and closer to a specific value, and the sequence must converge.
3. Rigorous Proof
- Existence of the Least Upper Bound (LUB): Since the sequence is bounded above, the set of its terms has an upper bound. By the completeness of the real numbers, this set has a least upper bound, say L.
-
Show that L is the Limit:
We want to show that for any ε > 0, there exists an N such that for all n ≥ N, |aₙ – L| < ε.
Since L is the least upper bound, any number smaller than L, like L – ε, cannot be an upper bound for the sequence. This means that there must be some term in the sequence, say aₙ with index N, that is greater than L – ε.
Since the sequence is non-decreasing, all subsequent terms (for n > N) must also be greater than L – ε. And since L is an upper bound, all terms must be less than or equal to L. Therefore, for all n ≥ N, the difference between aₙ and L is less than ε, so |aₙ – L| < ε.
This shows that the sequence gets arbitrarily close to L as n gets larger, so L is the limit of the sequence.
- Conclusion: The sequence converges to L.
In summary, the Monotonic Sequence Theorem can be understood both intuitively, as a series of points on a number line approaching a “wall,” and rigorously, using the completeness of the real numbers and the definition of convergence. It ensures that every bounded, monotonic sequence in the real numbers must converge, providing a powerful tool for understanding the behavior of sequences.
Visualizing the Proof of the Monotonic Sequence Theorem
The Monotonic Sequence Theorem is a foundational result in real analysis. Here’s how you can visualize the key parts of the proof:
1. Existence of the Least Upper Bound (LUB):
Imagine the terms of the sequence as points on a number line. Since the sequence is bounded above, there is a “wall” or barrier (an upper bound) that the terms cannot pass. The least upper bound (LUB) is the closest point to the terms that still acts as a barrier. It’s like the sequence is trying to reach this point but can never quite get there.
By the completeness of the real numbers, this LUB must exist, and we call it L.
2. Show that L is the Limit:
Now, we want to show that the sequence actually converges to L. To visualize this:
- Think of ε as a small gap or buffer around L. The sequence must get within this gap as n gets larger.
- Since L is the least upper bound, any number smaller than L, like L – ε, cannot be an upper bound. So there must be some term in the sequence that enters this gap.
- Since the sequence is non-decreasing, all subsequent terms must also enter this gap and stay there. They can’t go past L because L is an upper bound, but they must be greater than L – ε.
- This means that the sequence gets closer and closer to L, squeezing into the gap around L, and thus converging to L.
3. Conclusion:
The sequence converges to L. You can think of the sequence as a series of points on a number line, steadily approaching L but never going past it. The completeness of the real numbers ensures that L exists, and the non-decreasing nature of the sequence ensures that it converges to L.
This visualization helps to make the abstract concepts in the proof more concrete and relatable, providing a mental picture of what’s happening in the proof.
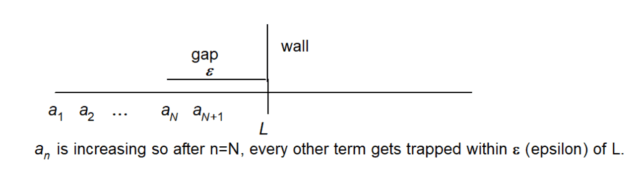
We can also visualize this as shown below.

