Bounded Above
A sequence (aₙ) is said to be bounded above if there exists a real number M such that aₙ ≤ M for all n ∈ ℕ. In other words, no term in the sequence is greater than M, and M is called an upper bound of the sequence.
Bounded Below
A sequence (aₙ) is said to be bounded below if there exists a real number m such that aₙ ≥ m for all n ∈ ℕ. In other words, no term in the sequence is less than m, and m is called a lower bound of the sequence.
Bounded
A sequence is simply called bounded if it is both bounded above and bounded below. This means that there exist real numbers M and m such that m ≤ aₙ ≤ M for all n ∈ ℕ. In this case, the sequence is confined within a fixed range, and no term can go to infinity or negative infinity.
These concepts are fundamental in real analysis and are used to study the properties of sequences and their convergence behavior.
Simple Examples: Bounded Above
A sequence that is bounded above has a limit to how high the numbers can go. For example, consider the sequence: 2, 4, 6, 8, 10. No number in this sequence is greater than 10, so we say it’s bounded above by 10.
Bounded Below
A sequence that is bounded below has a limit to how low the numbers can go. For example, consider the sequence: 5, 3, 4, 5, 6. No number in this sequence is less than 3, so we say it’s bounded below by 3.
Bounded
If a sequence is both bounded above and below, the numbers are trapped within a specific range. For example, consider the sequence: 7, 8, 7, 8, 7. The numbers in this sequence are never greater than 8 and never less than 7, so we say it’s bounded by 7 and 8.
Understanding whether a sequence is bounded helps mathematicians and scientists analyze patterns and make predictions. It’s like knowing the minimum and maximum temperatures for the day; you know how to dress because you know it won’t get too hot or too cold.
Bounded Above
A sequence that is bounded above has a limit to how high the numbers can go. Consider the sequence defined by the expression aₙ = 1/n, where n is a natural number starting from 1 (1, 2, 3, …).
This sequence looks like: 1/1, 1/2, 1/3, 1/4, 1/5, …
In this sequence, as n gets larger, the value of 1/n gets smaller. However, no matter how large n gets, the value of 1/n will never be greater than 1. So, we can say that this sequence is bounded above by 1.
This means that all the numbers in the sequence are less than or equal to 1, and 1 is the upper bound of the sequence.
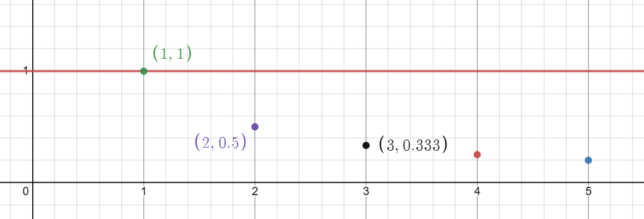
In the graph created in Desmos, the horizontal line y = 1 represents the upper bound for the sequence defined by aₙ = 1/n. Alongside this line, individual points are plotted for x = 1, x = 2, x = 3, x = 4, and x = 5, corresponding to the values (1, 1/1), (2, 1/2), (3, 1/3), (4, 1/4), and (5, 1/5) respectively. These points illustrate the values of the sequence and visually demonstrate how the terms of the sequence approach 0 as n increases, yet never exceed the value of 1. The graph effectively captures the idea that the sequence is bounded above by 1, providing a clear and intuitive visual representation of this mathematical concept.
Bounded Above and Increasing
Consider the sequence defined by the expression aₙ = n / (n + 1), where n is a natural number starting from 1 (1, 2, 3, …).
This sequence looks like: 1/2, 2/3, 3/4, 4/5, 5/6, …
In this sequence, as n gets larger, both the numerator and the denominator increase, but the value of n / (n + 1) gets closer and closer to 1. So, we can say that this sequence is bounded above by 1.
This means that all the numbers in the sequence are less than or equal to 1, and 1 is the upper bound of the sequence. Additionally, since each term is greater than the previous term, the sequence is increasing.
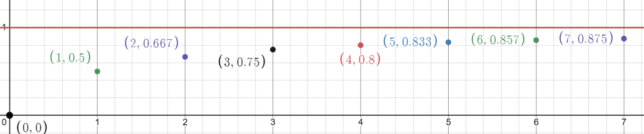
If you were to graph this sequence in Desmos, you would see the individual points for x = 1, x = 2, x = 3, x = 4, and x = 5, corresponding to the values (1, 1/2), (2, 2/3), (3, 3/4), (4, 4/5), and (5, 5/6) respectively, all lying below the horizontal line y = 1. This graph would visually demonstrate how the sequence is both bounded above by 1 and increasing.
An Upper Bound vs. The Upper Bound (Least Upper Bound)
Consider the sequence defined by the expression aₙ = n / (n + 1), where n is a natural number starting from 1.
This sequence looks like: 1/2, 2/3, 3/4, 4/5, 5/6, …
An Upper Bound
“An upper bound” refers to any number that is greater than or equal to every term in the sequence. For example, the numbers 2, 1.5, and 1 are all upper bounds for this sequence.
However, 0.8 is not an upper bound, as there are values in the sequence, like 4/5 (0.8) and 5/6 (approximately 0.833), that are equal to or greater than 0.8.
Values in the sequence:
- 1/2 is less than 2, 1.5, 1, and 0.8
- 2/3 is less than 2, 1.5, 1, and 0.8
- 3/4 is less than 2, 1.5, 1, and 0.8
- 4/5 is equal to 0.8 and less than 2, 1.5, and 1
- 5/6 is greater than 0.8 and less than 2, 1.5, and 1
The Upper Bound (Least Upper Bound)
“The upper bound” or “the least upper bound” (LUB) refers to the smallest number that is an upper bound for the sequence. In this case, the LUB is 1. There is no number smaller than 1 that is greater than or equal to every term in the sequence.
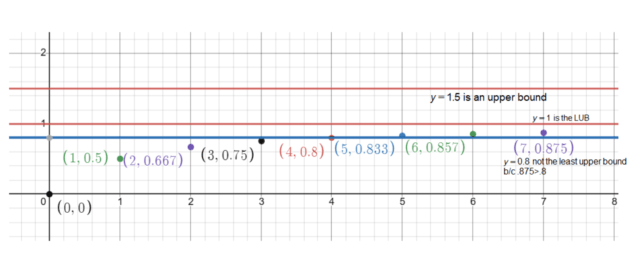
Your graph shows the lines y = 0.8, y = 1.5, and y = 1. The line y = 1 represents the LUB, while y = 0.8 is not an upper bound as some terms in the sequence are greater than 0.8. The line y = 1.5 represents another upper bound but is not the LUB as it is not the smallest upper bound.
Values in the sequence compared to the LUB:
- 1/2 is less than 1 (the LUB)
- 2/3 is less than 1 (the LUB)
- 3/4 is less than 1 (the LUB)
- 4/5 is less than 1 (the LUB)
- 5/6 is less than 1 (the LUB)
This distinction between “an upper bound” and “the upper bound” helps us understand how sequences behave and provides insights into their properties and limits.
Monotonic Increasing and Monotonic Decreasing Sequences
Monotonic Increasing
A sequence is said to be monotonic increasing if each term is greater than or equal to the previous term. An example of a monotonic increasing sequence is aₙ = n.
Values in the sequence:
- a₁ = 1
- a₂ = 2
- a₃ = 3
- a₄ = 4
- a₅ = 5
This sequence shows that each term is greater than the previous one: 1 < 2 < 3 < 4 < 5, and so on.
Monotonic Decreasing
A sequence is said to be monotonic decreasing if each term is less than or equal to the previous term. An example of a monotonic decreasing sequence is aₙ = 1 / n.
Values in the sequence:
- a₁ = 1
- a₂ = 1/2
- a₃ = 1/3
- a₄ = 1/4
- a₅ = 1/5
This sequence shows that each term is less than the previous one: 1 > 1/2 > 1/3 > 1/4 > 1/5, and so on.
Understanding whether a sequence is monotonic increasing or decreasing can provide insights into its behavior, convergence, and other properties. Monotonic sequences are often encountered in mathematical analysis and have applications in various fields.
Monotonic Increasing vs. Increasing
Monotonic Increasing
A sequence is said to be monotonic increasing if each term is greater than or equal to the previous term. In other words, the sequence can stay the same or increase, but it cannot decrease. The key here is that the sequence is allowed to have consecutive terms that are equal.
Example of a monotonic increasing sequence: 1, 2, 2, 3, 3, 3, 4, 5, …
Strictly Increasing
A sequence is said to be strictly increasing if each term is strictly greater than the previous term. Unlike monotonic increasing, a strictly increasing sequence cannot have consecutive terms that are equal; each term must be greater than the one before it.
Example of a strictly increasing sequence: 1, 2, 3, 4, 5, …
Comparison
While both monotonic increasing and strictly increasing sequences involve terms that get larger, the key difference lies in how they handle equality:
- Monotonic Increasing: Allows consecutive terms to be equal (e.g., 2, 2, 3).
- Strictly Increasing: Does not allow consecutive terms to be equal; each term must be greater than the previous one (e.g., 2, 3, 4).
It’s worth noting that all strictly increasing sequences are also monotonic increasing, but not all monotonic increasing sequences are strictly increasing.
Understanding these distinctions is important in mathematical analysis and other fields, as different properties and theorems may apply depending on whether a sequence is monotonic increasing or strictly increasing.
