Introduction to Series
A series is the sum of the terms of a sequence. It’s a way to represent and analyze the sum of infinitely many terms. While a sequence is a list of numbers, a series is the sum of those numbers.
A series is denoted by the summation symbol (Σ) and is defined as S = Σ (from n=1 to ∞) aₙ, where aₙ is the nth term of the sequence.
A partial sum is the sum of the first n terms of a series, denoted as Sₙ = Σ (from i=1 to n) aᵢ. The sequence of partial sums (Sₙ) provides insight into the behavior of the series and is a fundamental concept in understanding series.
Examples include the series defined by aₙ = n, aₙ = 1/n, and an oscillating series where aₙ alternates between -1 and 1. The total sum of a series is the limit of the sequence of partial sums, and this relationship helps us understand whether the series converges or diverges.
An important example is the geometric series, represented as Σ (from n=0 to N-1) arⁿ or Σ (from n=1 to ∞) ar^(n-1). Both representations produce the same terms, and the sum of a geometric series can be derived using specific formulas.
Shifting the index in summation notation involves changing the starting and ending values of the index and adjusting the expression inside the summation. For example, Σ (from n=0 to N-1) arⁿ can be shifted to Σ (from n=1 to N) ar^(n-1).
This introduction covers the essential concepts of series, including definitions, partial sums, examples, and techniques for working with series.
Introduction to Series
A series is the sum of the terms of a sequence. It’s a way to represent and analyze the sum of infinitely many terms. While a sequence is a list of numbers, a series is the sum of those numbers.
Definition of a Series
A series is denoted by the summation symbol and is defined as:
where is the nth term of the sequence.
Partial Sums
A partial sum is the sum of the first terms of a series. It is denoted as:
The sequence of partial sums provides insight into the behavior of the series and is a fundamental concept in understanding series.
Example of the Series Defined by aₙ = n
Consider the series defined by the sequence aₙ = n:
S = Σ (from n=1 to ∞) n = 1 + 2 + 3 + 4 + 5 + …
We can compute several partial sums to see how the series behaves:
- S₁ = Σ (from i=1 to 1) i = 1
- S₂ = Σ (from i=1 to 2) i = 1 + 2 = 3
- S₃ = Σ (from i=1 to 3) i = 1 + 2 + 3 = 6
- S₄ = Σ (from i=1 to 4) i = 1 + 2 + 3 + 4 = 10
- S₅ = Σ (from i=1 to 5) i = 1 + 2 + 3 + 4 + 5 = 15
The sequence of partial sums is a new sequence {S₁, S₂, S₃, …}, and the total sum of the series is the limit of this sequence of partial sums.
In this case, the sequence of partial sums grows without bound, so the limit does not exist. Therefore, the series is divergent, meaning that it does not converge to a specific value.
The relationship between the total sum of a series and the limit of the sequence of partial sums is a fundamental concept in the study of series. It helps us understand how the individual terms contribute to the overall sum and whether the series converges or diverges.
Example of the Series Defined by aₙ = 1/n
Consider the series defined by the sequence aₙ = 1/n:
S = Σ (from n=1 to ∞) 1/n = 1 + 1/2 + 1/3 + 1/4 + 1/5 + …
We can compute several partial sums to see how the series behaves:
- S₁ = Σ (from i=1 to 1) 1/i = 1
- S₂ = Σ (from i=1 to 2) 1/i = 1 + 1/2 = 1.5
- S₃ = Σ (from i=1 to 3) 1/i = 1 + 1/2 + 1/3 ≈ 1.833
- S₄ = Σ (from i=1 to 4) 1/i = 1 + 1/2 + 1/3 + 1/4 ≈ 2.083
- S₅ = Σ (from i=1 to 5) 1/i = 1 + 1/2 + 1/3 + 1/4 + 1/5 ≈ 2.283
The sequence of partial sums is a new sequence {S₁, S₂, S₃, …}, and the total sum of the series is the limit of this sequence of partial sums.
In this case, the sequence of partial sums continues to grow without bound as we add more terms, even though the individual terms are getting smaller. Therefore, the limit does not exist, and the series is divergent.
This series is known as the harmonic series, and its divergence is a classic result in mathematics. It illustrates how a series can diverge even if the individual terms are getting smaller and smaller.
Example of an Oscillating Series
Consider the series defined by the sequence , where each term alternates between -1 and 1:
We can compute several partial sums to see how the series behaves:
As we can see, the partial sums oscillate between 0 and 1, depending on whether the number of terms is even or odd. This pattern continues indefinitely, and the series does not settle down to a specific value.
This series is an example of a divergent series, meaning that it does not converge to a specific value. The oscillating behavior illustrates the importance of carefully considering the convergence or divergence of a series, especially when dealing with infinite sums.
Sum of a Series with Given Limit of Partial Sums
Suppose we have a series defined by the sequence aₙ, and we know that the limit of the partial sums (the sum of the first n terms) is given by:
lim (n → ∞) sₙ = 3n / (4n + 7)
Then the sum of the series, if it converges, is the limit of this expression as n approaches infinity:
Sum of series = lim (n → ∞) 3n / (4n + 7)
When dealing with limits as n approaches infinity, constants and lower-order terms often become insignificant relative to the leading terms. In this case, the constant 7 in the denominator becomes insignificant compared to the 4n term as n grows large.
So we can focus on the leading terms and write:
Sum of series ≈ lim (n → ∞) 3n / 4n
Now we can cancel the n’s:
Sum of series = lim (n → ∞) 3 / 4 = 3 / 4
So the sum of the series converges to 3/4.
This example illustrates how the limit of the sequence of partial sums can be used to find the sum of the series, and it highlights the idea that constants and lower-order terms can often be dropped when dealing with limits at infinity.
Two Representations of a Geometric Series
A geometric series can be represented in two different ways using summation notation, but both produce the same terms.
1. Starting from to :
This representation starts with and goes up to , where is the number of terms in the partial sum.
2. Starting from to :
This representation starts with and goes up to , and uses to produce the same terms as the first representation.
Comparison:
Both representations produce the same terms:
- When in the first representation, the term is .
- When in the second representation, the term is .
- Both continue with the same pattern:
These two representations show that the choice of indexing in summation notation can be flexible, and different choices can lead to the same series.
Shifting the Index in Summation Notation
Shifting the index in summation notation involves changing the starting and ending values of the index, as well as adjusting the expression inside the summation. Here’s how it works:
Original Representation (starting from ):
Shifting the Index (starting from ):
To shift the index from starting at to starting at , we need to make two adjustments:
- Adjust the Expression: Since goes from to , the expression has to decrease by . So, we replace with inside the expression: becomes .
- Adjust the Bounds: The starting value of changes from to , and the ending value changes from to : .
The result is a new representation that produces the same terms as the original:
This example illustrates that shifting the index is a flexible technique that can be used to change the appearance of a series without changing its value.


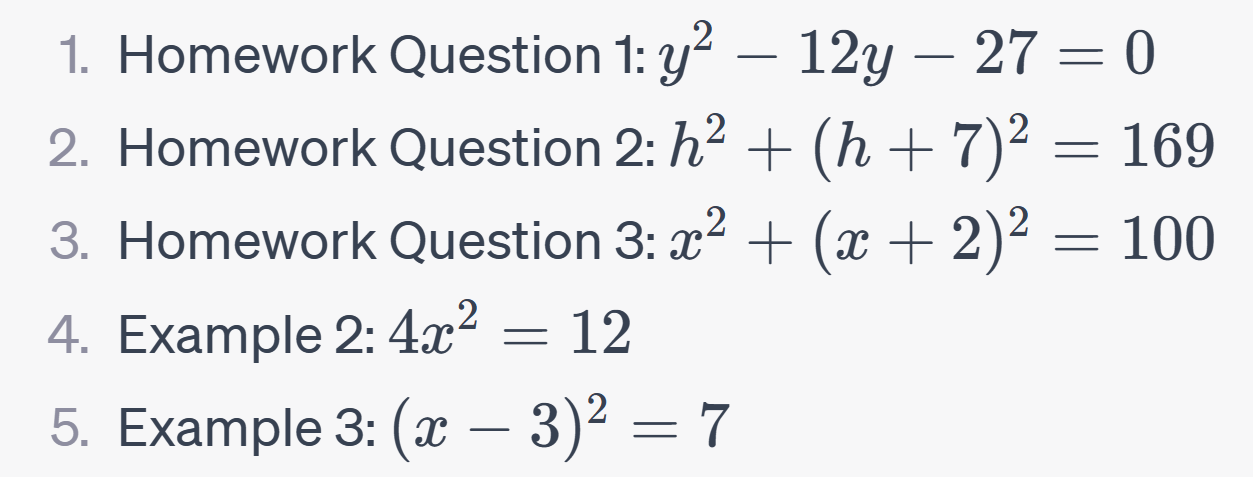
 Step 1: Rewrite the equation as 3y² – 12y – 27 = 0.
Step 1: Rewrite the equation as 3y² – 12y – 27 = 0. Step 2: Divide each term by 3 to get y² – 4y – 9 = 0.
Step 2: Divide each term by 3 to get y² – 4y – 9 = 0. Step 3: Use the quadratic formula to find the roots of the equation.
Step 3: Use the quadratic formula to find the roots of the equation.