Author: tom

The Harmonic Sequence

The harmonic sequence is a well-known mathematical sequence found in various fields. It is defined as the sequence of reciprocals of the natural numbers.

Definition

The harmonic sequence is defined by the formula \(a_n = \frac{1}{n}\), where \(n\) is a positive integer. The first few terms of the harmonic sequence are \(\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots\).

Properties

• Non-Constant Difference: The difference between consecutive terms is not constant. For example, \(\frac{1}{2} – \frac{1}{1} = -\frac{1}{2}\), but \(\frac{1}{3} – \frac{1}{2} = -\frac{1}{6}\).
• Monotonic Decreasing: Each term is smaller than the previous term, so the sequence is decreasing. As \(n\) grows, the terms get closer to zero.
• Convergence to Zero: As \(n\) approaches infinity, the terms \(\frac{1}{n}\) approach zero. This means that the limit of the sequence is zero.

Graphical Representation

The graph of the harmonic sequence shows a curve that approaches zero as \(n\) increases. It can be represented by the function \(y = \frac{1}{x}\), where \(x\) is a positive integer.

Applications

The harmonic sequence has various applications, including in physics, music, and engineering, where it helps in understanding wave patterns, overtones, and electrical circuits.

Summary

The harmonic sequence is an essential mathematical concept with unique properties and wide-ranging applications. Its behavior, where the terms decrease but never reach zero, makes it a fascinating subject of study.

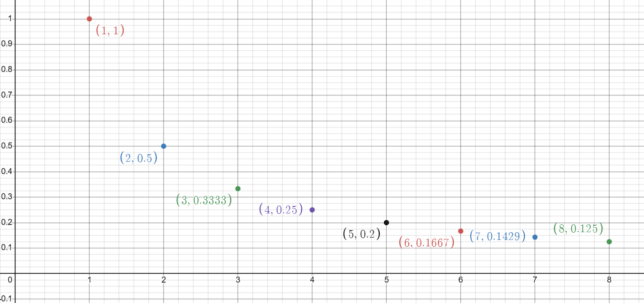
Dot Plot of the Sequence \( \frac{1}{n} \)

The dot plot of the sequence \( \frac{1}{n} \) for \( n = 1 \) to \( 8 \) shows a clear pattern of decay. As the value of \( n \) increases, the corresponding value of \( \frac{1}{n} \) decreases, approaching zero.

Specifically, the points plotted are:

• \( (1, 1) \)
• \( (2, \frac{1}{2}) \)
• \( (3, \frac{1}{3}) \)
• \( (4, \frac{1}{4}) \)
• \( (5, \frac{1}{5}) \)
• \( (6, \frac{1}{6}) \)
• \( (7, \frac{1}{7}) \)
• \( (8, \frac{1}{8}) \)

This pattern illustrates the fundamental property of the harmonic sequence, where each term is the reciprocal of its position in the sequence. The plot visually represents how the terms of the sequence get closer to zero as \( n \) increases, but never actually reach zero.

Deriving the Formula for the Sum of a Geometric Sequence (Part 1)

Consider a geometric sequence with n terms, first term a, and common ratio r:

  a, ar, ar², ..., ar(n-1)
  

We want to find a formula for the sum of this sequence, S:

  S = a + ar + ar² + ... + ar(n-1)
  

Step 1: Multiply the entire sequence by r

  rS = ar + ar² + ar³ + ... + arn
  

Step 2: Align S and rS vertically

  S  =  a + ar    + ar²  + ar³  + ... + ar(n-2) + ar(n-1)
  rS =     ar + ar²  + ar³  + ... + ar(n-2) + ar(n-1) + arn
  

Step 3: Subtract rS from S

Subtracting the sequences, we see that most terms cancel out:

  S - rS = (a + ar + ar² + ... + ar(n-1)) - (ar + ar² + ar³ + ... + arn)
          = a - arn
  

  S - rS = a - arn
  

  S(1 - r) = a - arn
  

  S = (a - arn) / (1 - r)
  

  S = a(1 - rn) / (1 - r)
  

Example: Sum of a Finite Geometric Sequence

Consider a geometric sequence with the first term \( a = 3 \), common ratio \( r = 2 \), and \( n = 5 \) terms:

  3, 6, 12, 24, 48
  

Step 1: Identify the values of a, r, and n

  a = 3, r = 2, n = 5
  

Step 2: Use the formula for the sum of a finite geometric sequence

The formula for the sum of a finite geometric sequence with n terms, first term a, and common ratio r is:

  S = a(1 - rn) / (1 - r)
  

Step 3: Substitute the values into the formula

  S = 3(1 - 25) / (1 - 2)
    = 3(1 - 32) / (-1)
    = 3(-31) / (-1)
    = 93
  

The sum of the first 5 terms of this geometric sequence is 93.

Note: This formula is specifically for finite geometric sequences. For an infinite geometric sequence with \( |r| < 1 \), the sum is given by \( S = a / (1 - r) \).

Example: Sum of a Finite Geometric Sequence with Fractional Common Ratio

Consider a geometric sequence with the first term a = 4, common ratio r = 1/2, and n = 6 terms:

  4, 2, 1, 1/2, 1/4, 1/8
  

Step 1: Identify the values of a, r, and n

  a = 4, r = 1/2, n = 6
  

Step 2: Use the formula for the sum of a finite geometric sequence

  S = a(1 - rⁿ) / (1 - r)
  

Step 3: Substitute the values into the formula

  S = 4(1 - (1/2)⁶) / (1 - 1/2)  # Substitute a, r, and n
    = 4(1 - (1/64)) / (1/2)      # Calculate (1/2)⁶
    = 4(63/64) / (1/2)           # Subtract 1/64 from 1
    = (4 * 63/64) / (1/2)        # Multiply 4 by 63/64
    = (4 * 63/64) * 2            # Divide by 1/2 is the same as multiplying by 2
    = 4 * 63/32                  # Simplify the fraction
    = 252/32                     # Multiply 4 by 63
    = 63/8                       # Divide by 4
    = 7.875                      # Divide 63 by 8
  

The sum of the first 6 terms of this geometric sequence is 63/8 or 7.875.

Example: Sum of a Finite Geometric Sequence with Decimal Common Ratio

Consider a geometric sequence where we want to explore the effect of a small common ratio, such as r = 0.1. This choice of r means that each term is 10% of the previous term, leading to a rapid decrease in the value of the terms. Let’s take the first term a = 5, common ratio r = 0.1, and n = 4 terms:

  5, 0.5, 0.05, 0.005  # Each term is 10% of the previous term
  

Step 1: Identify the values of a, r, and n

  a = 5, r = 0.1, n = 4  # First term is 5, common ratio is 0.1, and there are 4 terms
  

Step 2: Use the formula for the sum of a finite geometric sequence

  S = a(1 - rⁿ) / (1 - r)  # General formula for the sum of a finite geometric sequence
  

Step 3: Substitute the values into the formula

  S = 5(1 - 0.1⁴) / (1 - 0.1)  # Substitute a, r, and n
    = 5(1 - 0.0001) / 0.9      # Calculate 0.1⁴, which represents the ratio raised to the power of 4
    = 5(0.9999) / 0.9          # Subtract 0.0001 from 1
    = 4.9995 / 0.9             # Multiply 5 by 0.9999
    = 5.555                   # Divide 4.9995 by 0.9
  

The sum of the first 4 terms of this geometric sequence is 5.555. The choice of r = 0.1 leads to a sequence where each term is only 10% of the previous term, resulting in a quickly diminishing sequence.

Finding the Number of Terms \( n \) in a Geometric Sequence

Given the sum \( S \), the first term \( a \), and the common ratio \( r \), you can find the number of terms \( n \) using the following steps:

1. Start with the sum formula: \[ S = \frac{{a(1 – r^n)}}{{1 – r}} \]
2. Multiply both sides by \( 1 – r \): \[ S(1 – r) = a(1 – r^n) \]
3. Divide both sides by \( a \): \[ \frac{{S(1 – r)}}{a} = 1 – r^n \]
4. Rearrange to isolate \( r^n \): \[ r^n = 1 – \frac{{S(1 – r)}}{a} \]
5. Take the natural logarithm of both sides: \[ \ln(r^n) = \ln\left(1 – \frac{{S(1 – r)}}{a}\right) \]
6. Use the property of logarithms that \(\ln(x^y) = y \cdot \ln(x)\): \[ n \cdot \ln(r) = \ln\left(1 – \frac{{S(1 – r)}}{a}\right) \]
7. Solve for \( n \): \[ n = \frac{{\ln\left(1 – \frac{{S(1 – r)}}{a}\right)}}{{\ln(r)}} \]

Important Consideration

Keep in mind that the value of \( n \) should be a positive integer, as it represents the number of terms in the sequence. If you obtain a non-integer value for \( n \), such as 2.4, it may indicate one of the following:

• Inconsistency: The given information (sum, first term, common ratio) may be inconsistent, leading to an invalid result for \( n \).
• Problem Definition: The problem may not be well-defined, and additional information or constraints may be required to obtain a valid solution for \( n \).

Always verify the given information and ensure that the problem is properly defined before attempting to solve for \( n \) in a geometric sequence.

Understanding Arithmetic Sequences

An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. This difference is known as the common difference, denoted by d.

Example of an Arithmetic Sequence

Consider the sequence 2, 4, 6, 8, … Here, the common difference is d = 2, meaning each term is 2 greater than the previous term.

Sum of an Arithmetic Sequence

The sum of the first n terms of an arithmetic sequence can be found using a special formula. But how do we derive this formula?

Derivation of the Formula

Let’s start by writing down the sum of the sequence:

  S = a + (a + d) + (a + 2d) + ... + (a + (n-2)d) + (a + (n-1)d)
  

Now, we’ll write the same sequence in reverse order:

  S = (a + (n-1)d) + (a + (n-2)d) + ... + (a + 2d) + (a + d) + a
  

By adding these two lines together, we notice that each pair of terms adds up to the same value, namely \(a + (a + (n-1)d)\). Since there are n terms, we have:

  2S = n × (a + (a + (n-1)d))
  

Notice that we have doubled the sum of the sequence by adding it to itself. To find the actual sum, we need to divide by 2:

  S = n/2 × (2a + (n-1)d)
  

This division by 2 corrects for the doubling of the sum, giving us the correct formula for the sum of the arithmetic sequence. It’s a clever way to find the sum by taking advantage of the pattern in the sequence.

Real-World Application

Arithmetic sequences are commonly used in various real-world scenarios, such as calculating the total savings over time with regular deposits, predicting linear growth or decline, and more. Understanding how to find the sum of an arithmetic sequence can be a valuable skill in finance, economics, and other fields.

Application of Arithmetic Sequences: Saving Money

Arithmetic sequences can be applied to understand and model saving money over time. Let’s consider a simple saving plan where you decide to save a fixed amount of money every month.

Example: Saving for a Vacation

Suppose you want to go on a vacation in a year, and you need $1200 for the trip. You decide to save money every month by putting aside a fixed amount. Since there are 12 months in a year, you can model your saving plan as an arithmetic sequence.

Here’s how it works:

• First month: $100 (a = 100, the first term)
• Second month: $200 (a + d, where d = 100 is the common difference)
• Third month: $300 (a + 2d)
• …
• Twelfth month: $1200 (a + 11d, the 12th term)

This is an arithmetic sequence with a common difference of $100. We can use the formula for the sum of an arithmetic sequence to calculate the total amount saved:

  S = n/2 × (2a + (n-1)d) 
    = 12/2 × (2 × 100 + (12-1) × 100) 
    = 6 × (200 + 1100) 
    = 6 × 1300 
    = $7800
  

Explanation:

• n = 12 (number of terms)
• a = 100 (first term)
• d = 100 (common difference)
• 2a = 200 (twice the first term)
• (n-1)d = 1100 (common difference multiplied by one less than the number of terms)
• Sum = $7800 (total amount saved)

By following this saving plan, you will have $7800 saved by the end of the year, enough for your vacation and some extra spending money!

Conclusion

Arithmetic sequences provide a simple and effective way to model and understand saving plans, investments, and other financial scenarios. By understanding the pattern and using the formula for the sum, you can plan and predict your financial growth over time.

Sum of an Arithmetic Sequence Using Averages

The sum of an arithmetic sequence can also be calculated using the average of the first and last terms. This method is particularly useful when you know the first and last terms and the total number of terms in the sequence.

  S = n/2 × (a + l) 
    = 12/2 × (100 + 1200) 
    = 6 × 1300 
    = $7800
  

Explanation:

• n = 12 (number of terms)
• a = 100 (first term)
• l = 1200 (last term)
• a + l = 1300 (sum of the first and last terms)
• Sum = $7800 (total amount saved)

This method provides the same result as the previous formula and offers a different perspective on understanding arithmetic sequences.

Deriving the Formula for the Sum of an Arithmetic Sequence Using Averages and Last Term Expression

Consider an arithmetic sequence with \( n \) terms, first term \( a \), and common difference \( d \):

  a, a + d, a + 2d, ..., a + (n-1)d
  

The last term can be expressed as:

  l = a + (n-1)d
  

The sum of the sequence can be represented as:

  S = a + (a + d) + (a + 2d) + ... + a + (n-1)d
  

The average of the first and last terms is:

  Average = (a + (a + (n-1)d)) / 2
  

Multiply the average by the number of terms \( n \) to find the sum:

  S = n × Average
  

This formula provides a simple way to calculate the sum of an arithmetic sequence using the average of the first and last terms, the number of terms, and the common difference.

Definition and Explanation

In a geometric sequence, each term is the product of the previous term and a constant called the common ratio, denoted by r. Here’s how it works:

1st term: a (starting value)

2nd term: a × r (multiply the first term by r)

3rd term: a × r × r (multiply the second term by r)

And so on…

Example: In the sequence 2, 6, 18, 54, the common ratio is 3, as each term is 3 times the previous term.

General Formula

The general formula for the n-th term of a geometric sequence is:

aₙ = a × r^(n-1)

Explanation:

a = first term

r = common ratio (can be a fraction)

n = term number

(n-1) = number of times r is multiplied

Example with Fractional Common Ratio:

Consider the sequence 16, 8, 4, 2, where the common ratio is 1/2:

5th term = 16 × (1/2)⁴ = 16 × 1/2⁴ = 16 × 1/16 = 16/16 = 1

Working Through Examples

Let’s work through examples to understand the concept better.

Example 1: Finding the Common Ratio

Consider the sequence 5, 15, 45, 135:

r = 15 ÷ 5 = 3 (divide any term by the previous term)

Example 2: Using the General Formula

For the sequence 5, 10, 20, 40, find the 6th term:

a₆ =5 × 2⁽⁶⁻¹⁾ = 5 × 2⁵ = 5 × 32 = 160 (use the formula with a=5, r=2, n=6)

Application: Compound Interest

Geometric sequences are used to calculate compound interest in finance. Here’s how it works:

Initial Investment: P

Annual Interest Rate: r

Number of Years: n

The amount after n years, A, is given by the formula:

A = P × (1 + r)ⁿ

Example:

If you invest $1000 with an annual interest rate of 10%, compounded annually, for 3 years:

P = $1000, r = 0.10, n = 3

A = $1000 × (1 + 0.10)³ = $1000 × 1.10³ = $1331

Your investment grows to $1331 in 3 years.

Derivation of the General Formula for a Geometric Sequence

Let’s explore why the formula for the n-th term of a geometric sequence is a × r^(n-1) and not a × rⁿ.

Consider a geometric sequence with a common ratio of r:

1st term: a (starting value)

2nd term: a × r (multiply the first term by r)

3rd term: a × r² (multiply the second term by r)

4th term: a × r³ (multiply the third term by r)

And so on…

Notice that the exponent in each term is one less than the term number. This pattern continues for all terms in the sequence.

General Formula:

The n-th term can be expressed as:

a_n = a × r^(n-1)

Explanation:

a = first term (starting value)

r = common ratio

n = term number

(n-1) = number of times r is multiplied (one less than the term number)

Example:

For the sequence 3, 6, 12, 24, the common ratio is 2, and the 4th term is:

a₄ = 3 × 2³ = 3 × 8 = 24

This derivation helps us understand why the formula includes r^(n-1) and not rⁿ, reflecting the pattern observed in geometric sequences.

Exponential Decay Sequence: (1/2)⁽ⁿ⁻¹⁾

This sequence is defined by the formula (1/2)⁽ⁿ⁻¹⁾, where n represents the term number.

The plot above shows the values of the sequence for n = 1, 2, 3, 4, 5. The values decrease by half with each successive term, illustrating exponential decay.

The horizontal axis (labeled “n”) represents the term number, while the vertical axis (labeled “Value”) represents the value of the term.

Exponential Growth Sequence: 2⁽ⁿ⁻¹⁾

This sequence is defined by the formula 2⁽ⁿ⁻¹⁾, where n represents the term number.

The plot above shows the values of the sequence for n = 1, 2, 3, 4, 5. The values double with each successive term, illustrating exponential growth.

The horizontal axis (labeled “n”) represents the term number, while the vertical axis (labeled “Value”) represents the value of the term.

Finding the Term Number in an Arithmetic Sequence

Consider an arithmetic sequence where the common difference is d = 5, and we know the value of a specific term is aₙ = 40. However, we do not know the term number n. The first term of the sequence is a = 10. Let’s find the value of n.

Problem Statement

Given an arithmetic sequence with a = 10, d = 5, and aₙ = 40, find the term number n for which the value of the term is 40.

Solution

We can use the formula for the n-th term of an arithmetic sequence:

aₙ = a + (n – 1) × d (General formula)

40 = 10 + (n – 1) × 5 (Substitute given values)

40 = 10 + 5n – 5 (Distribute the 5)

35 = 5n (Combine like terms)

n = 7 (Divide by 5 to solve for n)

So the term number for which the value of the term is 40 is n = 7.

Conclusion

In this arithmetic sequence, the 7th term has the value 40. This example demonstrates how to find the term number when the term value and common difference are known, but the term number is unknown. The step-by-step explanation helps beginners understand the process of solving the problem.

Arithmetic Sequences with Negative Common Difference

An arithmetic sequence can have a negative common difference, meaning that each term decreases by a constant amount. Let’s explore an example of such a sequence.

Example: Sequence 10, 7, 4, 1, -2

Consider the arithmetic sequence 10, 7, 4, 1, -2. In this sequence, the first term is \(a = 10\), and the common difference is \(d = -3\), as each term decreases by 3.

Derivation of the Formula

We can derive the formula for the \(n\)-th term of this sequence as follows:

\(a_n = a + (n – 1) \cdot d = 10 + (n – 1) \cdot (-3) = 10 – 3n + 3 = 13 – 3n\)

So the formula for the \(n\)-th term of this specific arithmetic sequence is \(a_n = 13 – 3n\).

Using the Formula to Find Specific Terms

Example: Using the derived formula, we can find any term in the sequence 10, 7, 4, 1, -2. For instance, the 4th term is:

\(a_4 = 13 – 3 \cdot 4 = 13 – 12 = 1\)

This demonstrates how the pattern in the sequence leads to the simplified formula, and how that formula can be used to find specific terms, even when the common difference is negative.

Applications

Arithmetic sequences with negative common differences can model situations of constant decline, such as depreciation of assets, cooling of a hot object, or decreasing sales. Understanding these sequences is essential in various real-world applications.

Finding the Term Number in an Arithmetic Sequence

Consider an arithmetic sequence where the common difference is d = 5, and we know the value of a specific term is aₙ = 40. However, we do not know the term number n. The first term of the sequence is a = 10. Let’s find the value of n.

Problem Statement

Given an arithmetic sequence with a = 10, d = 5, and aₙ = 40, find the term number n for which the value of the term is 40.

Solution

We can use the formula for the n-th term of an arithmetic sequence:

aₙ = a + (n – 1) × d

Substituting the given values, we have:

40 = 10 + (n – 1) × 5

40 = 10 + 5n – 5

35 = 5n

n = 7

So the term number for which the value of the term is 40 is n = 7.

Conclusion

In this arithmetic sequence, the 7th term has the value 40. This example demonstrates how to find the term number when the term value and common difference are known, but the term number is unknown.

Deriving the Formula for the n-th Term of an Arithmetic Sequence

An arithmetic sequence is a sequence of numbers where the difference between consecutive terms is constant. This difference is called the common difference, denoted by d.

First Few Terms

Let’s write down the first few terms of an arithmetic sequence:

• 1st term: a (the first term itself)
• 2nd term: a + d (one common difference added)
• 3rd term: a + 2d (two common differences added)
• 4th term: a + 3d (three common differences added)
• And so on…

Generalizing the Pattern

We can see a pattern emerging. The n-th term is the first term plus the common difference multiplied by one less than the term number. This “one less” comes from the fact that we start with the first term itself (a) and then add the common difference (d) (n-1) times.

Formula for the n-th Term

By generalizing this pattern, we can write the formula for the n-th term as:

aₙ = a + (n – 1) × d

Conclusion

This formula allows us to find any term in the arithmetic sequence if we know the first term (a), the common difference (d), and the term number (n). The (n-1) in the formula represents the fact that we add the common difference (n-1) times to the first term to reach the n-th term.

Arithmetic Sequence: (0,2), (1,4), (2,6), (3,8)

This arithmetic sequence represents a pattern where each term increases by 2. The coordinates (0,2), (1,4), (2,6), (3,8) correspond to the terms of the sequence. The first value in each pair (0, 1, 2, 3) represents the index or position of the term in the sequence, and it is plotted on the horizontal axis. The second value in each pair (2, 4, 6, 8) represents the value of the term itself, and it is plotted on the vertical axis.

The numbers are presented as integers (2, 4, 6, 8) rather than decimal numbers (2.0, 4.0, 6.0, 8.0) because the sequence follows a pattern of whole numbers. In mathematics, it is common to use the simplest form of a number, so integers are used when decimal places are not needed.

The plot below illustrates this sequence as discrete points, showing the linear relationship between the terms:

The arithmetic sequence is a fundamental concept in mathematics, often used to model linear growth or to describe patterns that follow a constant difference. In this case, the constant difference is 2, meaning that each term is 2 greater than the previous term.

Geometric Sequence: (0,1), (1,3), (2,9), (3,27)

This geometric sequence represents a pattern where each term is multiplied by 3. The coordinates (0,1), (1,3), (2,9), (3,27) correspond to the terms of the sequence. The first value in each pair (0, 1, 2, 3) represents the index or position of the term in the sequence, and it is plotted on the horizontal axis. The second value in each pair (1, 3, 9, 27) represents the value of the term itself, and it is plotted on the vertical axis.

The numbers are presented as integers because the sequence follows a pattern of whole numbers, and there are no fractional parts in these terms.

The plot below illustrates this sequence as discrete points, showing the exponential growth pattern between the terms:

The geometric sequence is a fundamental concept in mathematics, often used to model exponential growth or decay, or to describe patterns that follow a constant multiplication factor. In this case, the constant multiplication factor is 3, meaning that each term is 3 times greater than the previous term.

Fibonacci Sequence: (0,1), (1,2), (2,3), (3,5), (4,8), (5,13)

This sequence represents the famous Fibonacci pattern, where each term is the sum of the two preceding terms. The coordinates (0,1), (1,2), (2,3), (3,5), (4,8), (5,13) correspond to the terms of the sequence. The first value in each pair (0, 1, 2, 3, 4, 5) represents the index or position of the term in the sequence, and it is plotted on the horizontal axis. The second value in each pair (1, 2, 3, 5, 8, 13) represents the value of the term itself, and it is plotted on the vertical axis.

The numbers are presented as integers, reflecting the whole number nature of the Fibonacci sequence.

The plot below illustrates this sequence as discrete points, showing the growth pattern between the terms:

The Fibonacci sequence is a fundamental concept in mathematics, often found in nature and art, and used to model growth patterns and various phenomena. It follows a recursive pattern where each term is the sum of the two preceding terms.

Exponential Decay Sequence: (0,8), (1,4), (2,2), (3,1)

This sequence represents an exponential decay pattern, where each term is halved. The coordinates (0,8), (1,4), (2,2), (3,1) correspond to the terms of the sequence. The first value in each pair (0, 1, 2, 3) represents the index or position of the term in the sequence, and it is plotted on the horizontal axis. The second value in each pair (8, 4, 2, 1) represents the value of the term itself, and it is plotted on the vertical axis.

The numbers are presented as integers, reflecting the whole number nature of this sequence.

The plot below illustrates this sequence as discrete points, showing the exponential decay pattern between the terms:

The exponential decay sequence is a fundamental concept in mathematics, often used to model decay, depreciation, or reduction patterns in various contexts. It follows a pattern where each term is a fixed fraction (in this case, one-half) of the previous term.

Understanding Notation and Terminology in Sequences

When we talk about sequences, we use special symbols and words to describe them. Let’s break down some of the common notation and terminology used in sequences:

1. Terms of a Sequence

The individual numbers in a sequence are called “terms.” Think of them as the items in a list. For example, in the sequence 2, 4, 6, 8, …, the numbers 2, 4, 6, and 8 are the terms of the sequence.

2. Notation for Terms

We often use letters with small numbers below them to represent the terms of a sequence. Here’s an example:

a₁ means the first term, which could be 2

a₂ means the second term, which could be 4

a₃ means the third term, which could be 6

We can use \( a_n \) to represent any term in the sequence, where \( n \) is the position of the term.

3. Finite and Infinite Sequences

A “finite sequence” has a specific number of terms, like a list with an end. An “infinite sequence” goes on forever, like a never-ending list. When we use “…” at the end of a sequence, like 1, 2, 3, 4, …, it means the pattern continues without end.

4. Arithmetic and Geometric Sequences

There are special names for sequences that follow certain patterns:

Arithmetic Sequence: The difference between each term is the same. Example: 5, 10, 15, … (the difference is 5 each time)

Geometric Sequence: Each term is multiplied by the same amount. Example: 2, 4, 8, … (each term is multiplied by 2)

These concepts help us talk about sequences and understand how they work. They are like the building blocks for learning more about patterns in numbers. If you’re curious to learn more, keep reading, and we’ll explore more exciting topics in the world of sequences!

Real-World Examples of Sequences

Sequences are not just abstract mathematical concepts; they can be found all around us in the real world. Let’s explore some everyday examples of different types of sequences:

1. Arithmetic Sequence: Saving Money

If you save $10 more each month than the previous month, you are following an arithmetic sequence. Here’s how it might look:

Month 1: $10

Month 2: $20 (10 + 10)

Month 3: $30 (20 + 10)

And so on…

The difference between each month’s savings is $10.

2. Geometric Sequence: Population Growth

If a population of bacteria doubles every hour, it follows a geometric sequence. Here’s an example:

Hour 1: 100 bacteria

Hour 2: 200 bacteria (100 × 2)

Hour 3: 400 bacteria (200 × 2)

And so on…

Each hour, the population is multiplied by 2.

3. Fibonacci Sequence: Flower Petals

The Fibonacci sequence can be found in nature, such as in the arrangement of flower petals. Many flowers have a number of petals that is a term in the Fibonacci sequence:

3 petals: lily

5 petals: rose

8 petals: delphinium

And so on…

The number of petals often follows the pattern 0, 1, 1, 2, 3, 5, …

These real-world examples show that sequences are not just theoretical ideas but practical tools that help us understand and describe patterns in nature, finance, biology, and more. By studying sequences, we can gain insights into the world around us and make predictions about future events. Stay tuned for more exciting explorations into the world of sequences!

Understanding Sequences: A Beginner’s Guide

A sequence is a list of numbers that follows a specific pattern. Let’s explore some common types of sequences and see how they work:

1. Arithmetic Sequence

In an arithmetic sequence, the difference between each number is the same. Here’s an example:

2, 4, 6, 8, …

The difference between each number is 2:

4 – 2 = 2

6 – 4 = 2

8 – 6 = 2

And so on…

2. Geometric Sequence

In a geometric sequence, each number is multiplied by the same amount to get the next one. Here’s an example:

3, 6, 12, 24, …

Each number is multiplied by 2 to get the next one:

3 × 2 = 6

6 × 2 = 12

12 × 2 = 24

And so on…

3. Fibonacci Sequence

In the Fibonacci sequence, each number is the sum of the two before it. Here’s an example:

0, 1, 1, 2, 3, 5, …

Here’s how it works:

0 + 1 = 1

1 + 1 = 2

1 + 2 = 3

2 + 3 = 5

And so on…

Sequences are fascinating and can be found in many areas of mathematics and the real world. Whether it’s the rhythmic pattern of music, the growth of a population, or the spiraling of a seashell, sequences help us understand and describe these patterns. Stay tuned for more exciting insights into the world of sequences!

Integration by Parts using Tabular Approach

Let’s find the integral of x²eˣ using the tabular method:

1. Choose Functions:
• u = x²
• dv = eˣ dx
2. Create a Table:

For the table, alternate between differentiating u and integrating dv. Start by listing u, its successive derivatives, and dv, its successive integrals:

u	dv
x²	eˣ
2x	eˣ
2	eˣ

3. Apply Signs and Multiply Diagonally:

Now, apply alternating signs down the table. Multiply the terms diagonally and add them up:

(+) × (x²eˣ) + (-) × (2xeˣ) + (+) × (2eˣ)

Here’s how the multiplication works:

• First row: (+) × (x²eˣ) = x²eˣ
• Second row: (-) × (2xeˣ) = -2xeˣ
• Third row: (+) × (2eˣ) = 2eˣ
4. Final Result:

The integral of x²eˣ is:

∫ x²eˣ dx = x²eˣ – 2xeˣ + 2eˣ + C

where C is the constant of integration.