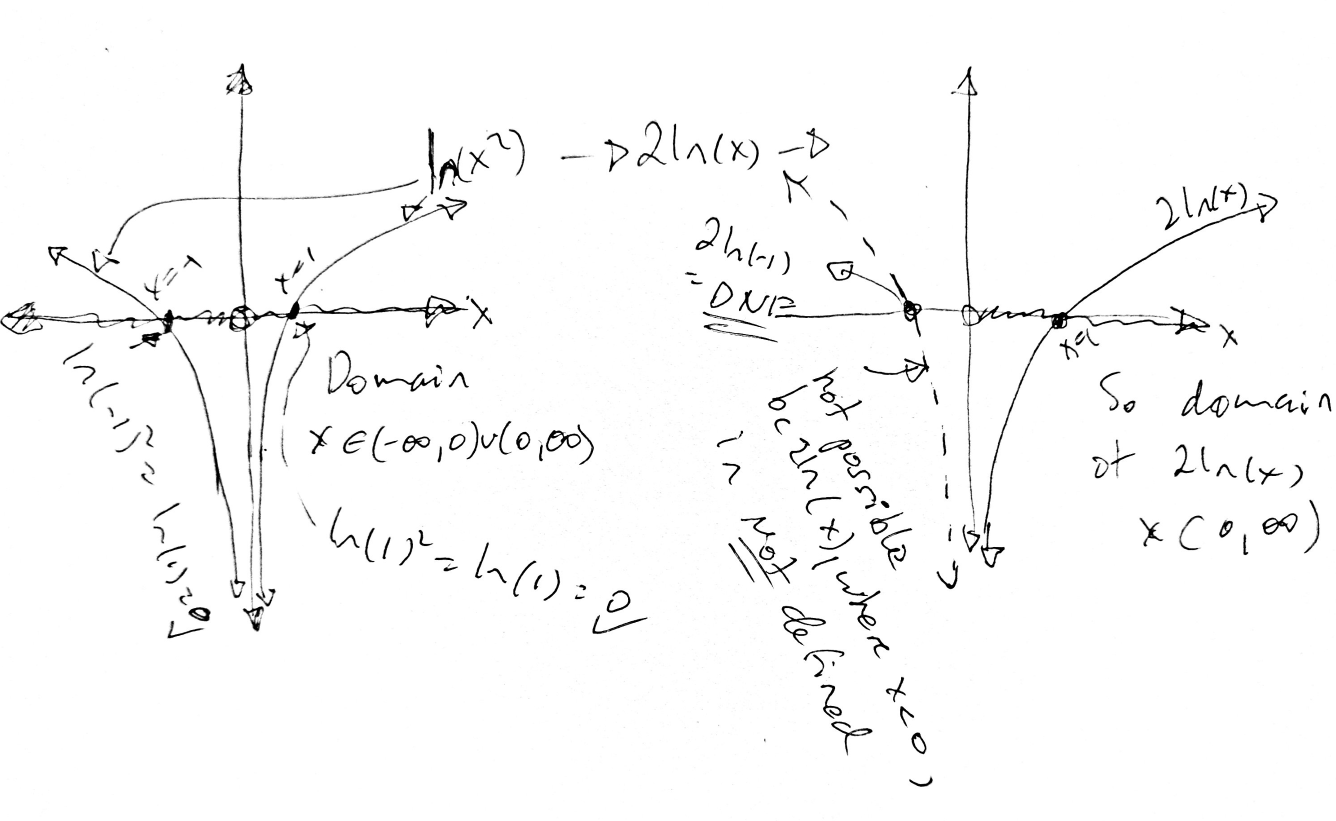
Domain of ln(x²):
——————————
The argument of the logarithm function x² must be positive. This is true for any x except zero, so the domain of ln(x²) is all real numbers except zero: x ∈ (−∞, 0) ∪ (0, +∞).
Example:
– For x = −2, x² = 4. ln(4) is valid.
– For x = 3, x² = 9. ln(9) is valid.
– For x = 0, x² = 0 and ln(0) is not defined.
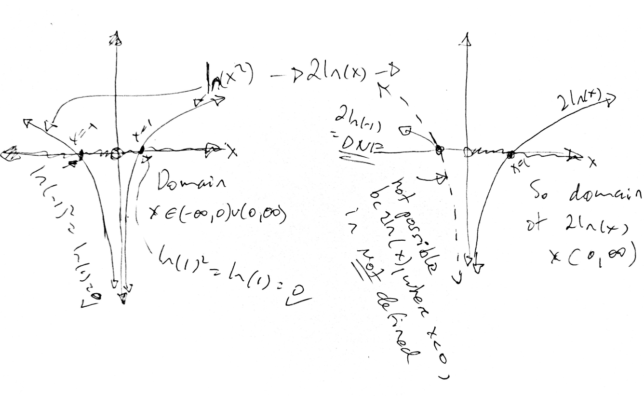
Domain of 2ln(x):
——————————
The argument x must be positive, so the domain is only positive real numbers: x ∈ (0, +∞).
Example:
– For x = 1, 2ln(1) = 2 × 0 = 0.
– For x = 5, 2ln(5) is valid.
– For x = −3 or x = 0, 2ln(−3) and 2ln(0) are not defined.
Conclusion:
——————————
ln(x²) is defined for any nonzero x, while 2ln(x) is only defined for positive x. Despite their algebraic similarities, they are distinct in terms of domain. ln(x²) can handle negative inputs because squaring them results in a positive number suitable for the log function. In contrast, 2ln(x) does not permit negative or zero inputs.