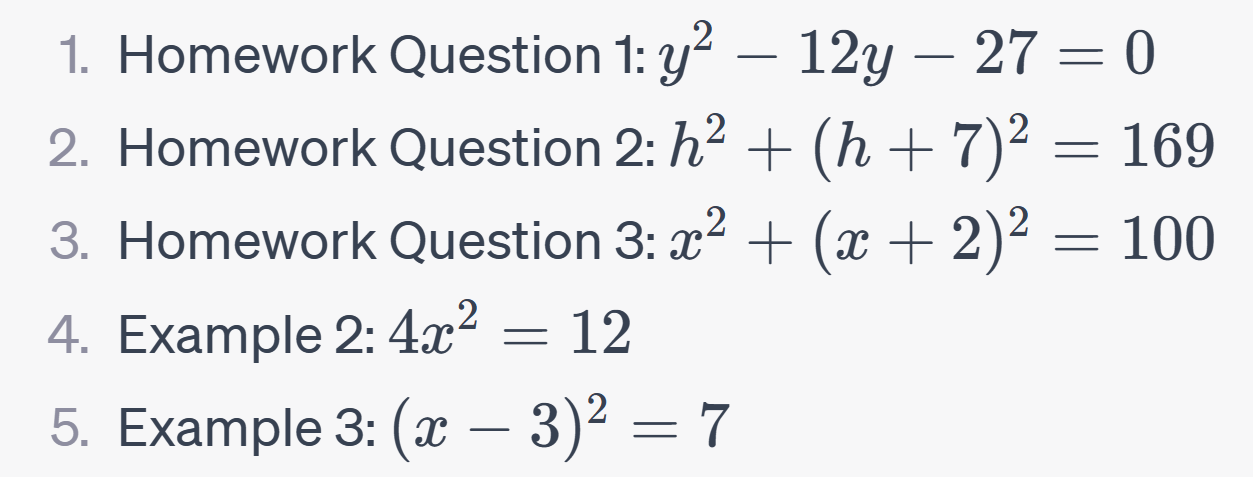Homework Question 1: Solving a Quadratic Equation
Given the equation 3y² – 12y = 27, the goal is to find the values of y that satisfy it.
1️⃣ Step 1: Rewrite the equation as 3y² – 12y – 27 = 0.
2️⃣ Step 2: Divide each term by 3 to get y² – 4y – 9 = 0.
3️⃣ Step 3: Use the quadratic formula to find the roots of the equation.
y = (-(-4) ± √((-4)² – 4 × 1 × -9)) / (2 × 1)
y = (4 ± √(16 + 36)) / 2
y = (4 ± √52) / 2
y = (4 ± 2√13) / 2
y = 2 ± √13
The solutions are y = 2 + √13 and y = 2 – √13.
Homework Question 2: Calculating the Height of a Rectangle with a Given Diagonal
In this problem, we have a rectangle with a diagonal that measures 13 inches. The width of the rectangle is 7 inches more than its height. We need to find out what the height is.
Step 1: Define the Variables
Let h be the height of the rectangle in inches. According to the problem, the width w is 7 inches more than the height. So, w = h + 7.
Step 2: Apply the Pythagorean Theorem
The Pythagorean theorem tells us that in a right-angled triangle, a² + b² = c². Here, a and b are the lengths of the legs and c is the length of the hypotenuse. In our rectangle, one leg is the height h, the other leg is the width w, and the hypotenuse is the diagonal, which is 13 inches. So, the equation is h² + w² = 169.
Step 3: Substitute and Simplify
We know w = h + 7, so we substitute this into the equation h² + w² = 169.
This gives us h² + (h + 7)² = 169.
Expand the square term (h + 7)² to get h² + 14h + 49.
Combine like terms to get 2h² + 14h + 49 = 169.
Subtract 169 from both sides to set the equation to zero: 2h² + 14h – 120 = 0.
Divide each term by 2 to simplify: h² + 7h – 60 = 0.
Step 4: Factor the Quadratic Equation
Factor the equation h² + 7h – 60 = 0 into (h – 5)(h + 12) = 0.
Solve for h to get h = 5 or h = -12.
Step 5: Choose the Valid Solution
Height can’t be negative, so the only valid solution is h = 5 inches.
Conclusion
The height of the rectangle is 5 inches.
Homework Question 3: Finding the Missing Sides of a Right Triangle
In this question, we have a right triangle with a hypotenuse that measures 10 inches. The difference between the other two sides is 2 inches. We are tasked with finding the lengths of these missing sides.
Step 1: Define the Variables
Let’s call one leg of the triangle x and the other leg x + 2. The hypotenuse is given as 10 inches.
Step 2: Use the Pythagorean Theorem
According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In mathematical terms, this is a² + b² = c². For our triangle, this becomes x² + (x + 2)² = 10² or x² + (x + 2)² = 100.
Step 3: Expand and Simplify
Expand the square term (x + 2)² to get x² + 4x + 4.
Combine like terms: x² + x² + 4x + 4 = 100.
Simplify further: 2x² + 4x + 4 = 100.
Subtract 100 from both sides: 2x² + 4x – 96 = 0.
Divide each term by 2: x² + 2x – 48 = 0.
Step 4: Factor the Equation
Factor the equation x² + 2x – 48 = 0 into (x – 6)(x + 8) = 0.
Solve for x to get x = 6 or x = -8.
Step 5: Choose the Valid Solution
Lengths can’t be negative, so the only valid solution for x is 6 inches. The other leg would then be 6 + 2 = 8 inches.
Conclusion
The lengths of the missing sides are 6 inches and 8 inches.
Example 2: Solving Quadratic Equations with Square Roots
In this example, we are dealing with the equation 4x² = 12. Our aim is to find the value or values of x.
Step 1: Divide by 4
The first step is to divide both sides of the equation by 4 to simplify it. This results in x² = 3.
Step 2: Take the Square Root
To isolate x, we take the square root of both sides. It’s important to remember that when you take the square root of both sides of an equation, you must consider both the positive and negative roots. This leads us to x = ±√3.
Step 3: Identify the Solutions
Now we have two possible solutions for x: x = √3 and x = -√3.
Conclusion
The equation 4x² = 12 has two solutions: x = √3 and x = -√3.
Example 3: Solving Quadratic Equations with Binomial Squares
In this example, the equation we have is (x – 3)² = 7. Our goal is to find the value or values of x.
Step 1: Take the Square Root
To isolate x, we take the square root of both sides of the equation. Remember to consider both the positive and negative roots. This gives us x – 3 = ±√7.
Step 2: Solve for x
Add 3 to both sides to solve for x: x = 3 ± √7.
Step 3: Identify the Solutions
Now we have two possible solutions for x: x = 3 + √7 and x = 3 – √7.
Conclusion
The equation (x – 3)² = 7 has two solutions: x = 3 + √7 and x = 3 – √7.