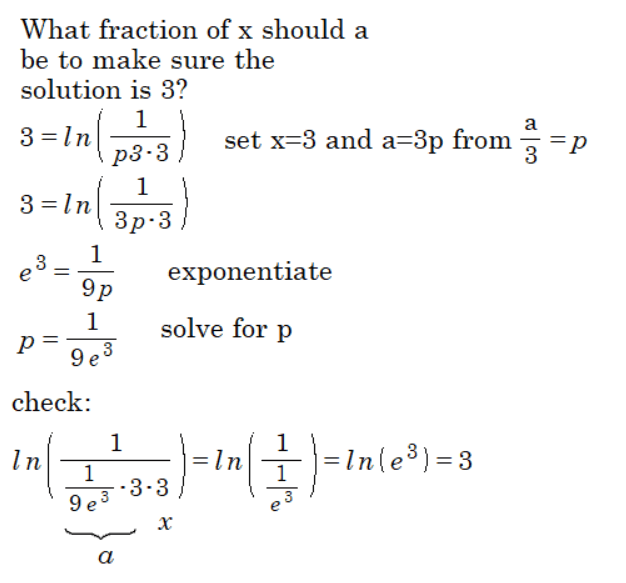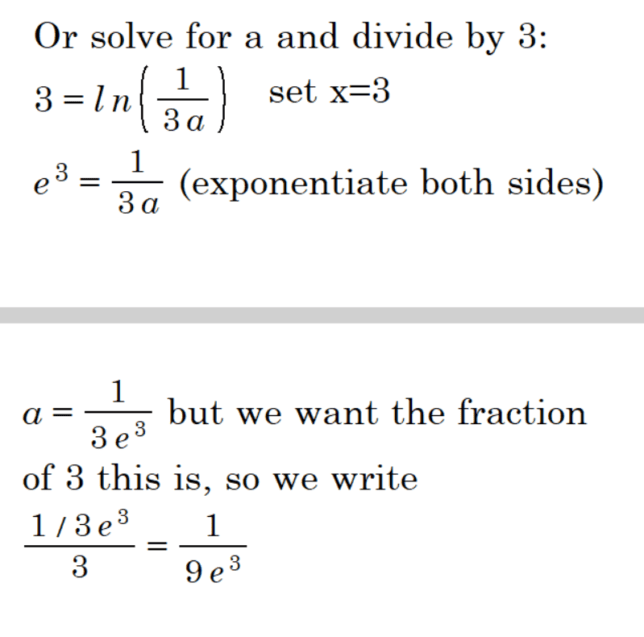Locus of |z − (1 + i)| = 1
What “locus” means: a locus is the set of all points that satisfy a given condition.

helps with math problems
What “locus” means: a locus is the set of all points that satisfy a given condition.
Little slope-triangles along f: base Δx, height Δy ≈ f′(xᵢ)Δx. Summing the vertical legs gives Δf.
Intuition. Over a tiny step Δx the curve is nearly straight, so f(x+Δx) ≈ f(x)+f′(x)·Δx. Slope turns “run” into “rise”. Each triangle’s height is that rise; adding them from a to b gives the net change f(b)−f(a). Errors come from curvature and are ≈(Δx)² per slice, so total error → 0 as Δx → 0.
Below is a detailed table contrasting Bart Ehrman’s common arguments against the resurrection with logical, historical, and metaphysical counterpoints. Each entry expands on the reasoning behind the claim and response to help readers engage more deeply with the issue.
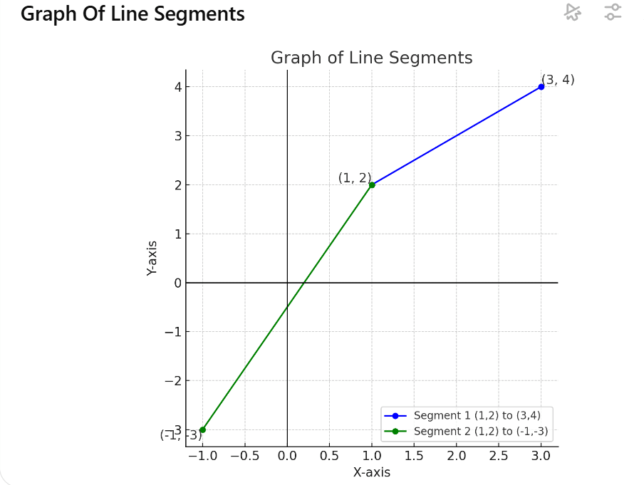
Use the distance formula between two points:
Distance = √((x₂ – x₁)² + (y₂ – y₁)²)
For points (1, 2) and (3, 4):
Length₁ = √((3 – 1)² + (4 – 2)²)
Simplify the differences:
Length₁ = √(2² + 2²)
Calculate the squares:
Length₁ = √(4 + 4)
Add the results:
Length₁ = √8
Approximate the square root:
Length₁ ≈ 2.828
Use the distance formula again for points (1, 2) and (-1, -3):
Length₂ = √((-1 – 1)² + (-3 – 2)²)
Simplify the differences:
Length₂ = √((-2)² + (-5)²)
Calculate the squares:
Length₂ = √(4 + 25)
Add the results:
Length₂ = √29
Approximate the square root:
Length₂ ≈ 5.385
Use the formula for the ratio of the two lengths:
Ratio = Length₂ ÷ Length₁
Substitute the approximate values:
Ratio = 5.385 ÷ 2.828
Perform the division:
Ratio ≈ 1.904
Thus, the approximate ratio of the lengths is 1.904.
To find the fraction of x that a must be to ensure the solution is 3, consider this:
Thus, the fraction of x that a must be to ensure the solution is 3 is 1/(9 * e^3).