Posted on

Step by Step Exercises on Finding the Modulus of a Complex Number

Welcome to our comprehensive guide on Modulus Calculation for Complex Numbers. This resource provides step-by-step instructions on how to calculate the modulus of various complex numbers, including both real and imaginary components. We cover examples such as 3 + 2i, -4 + 5i, -2 – 3i, and even pure real and imaginary numbers like 2 and 2i. Each example is broken down into easy-to-follow steps, from squaring the real and imaginary parts to taking the square root of their sum. We also provide reminders and tips, such as not including ‘i’ when calculating moduli. This guide is perfect for students, teachers, and anyone interested in enhancing their understanding of complex numbers and their moduli.

Modulus Calculation for Complex Numbers

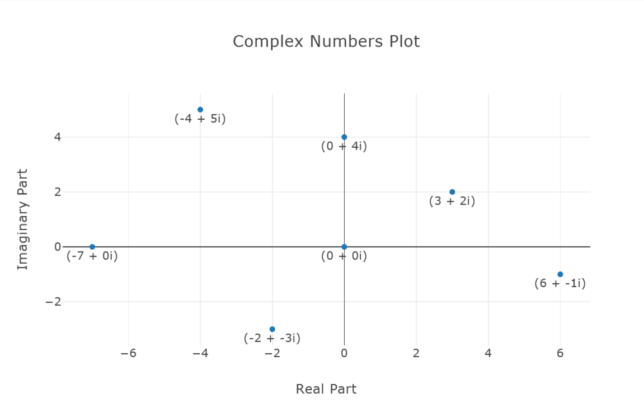
Calculating the Modulus of $3 + 2i$:

Learn how to calculate the modulus of the complex number $3 + 2i$ step by step:

  1. Calculate the square of the real part (3): $3^2 = 9$
  2. Calculate the square of the imaginary part (2): $2^2 = 4$
  3. Add the squares of the real and imaginary parts: $9 + 4 = 13$
  4. Take the square root of the sum: $\sqrt{13} \approx 3.60555$

The modulus of $3 + 2i$ is approximately $3.60555$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{3^2 + 2^2} \approx 3.60555$

Calculating the Modulus of $-4 + 5i$:

Learn how to calculate the modulus of the complex number $-4 + 5i$ step by step:

  1. Calculate the square of the real part (-4): $(-4)^2 = 16$
  2. Calculate the square of the imaginary part (5): $5^2 = 25$
  3. Add the squares of the real and imaginary parts: $16 + 25 = 41$
  4. Take the square root of the sum: $\sqrt{41} \approx 6.40312$

The modulus of $-4 + 5i$ is approximately $6.40312$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{(-4)^2 + 5^2} \approx 6.40312$

Calculating the Modulus of $-2 – 3i$:

Learn how to calculate the modulus of the complex number $-2 – 3i$ step by step:

  1. Calculate the square of the real part (-2): $(-2)^2 = 4$
  2. Calculate the square of the imaginary part (-3): $(-3)^2 = 9$
  3. Add the squares of the real and imaginary parts: $4 + 9 = 13$
  4. Take the square root of the sum: $\sqrt{13} \approx 3.60555$

The modulus of $-2 – 3i$ is approximately $3.60555$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{(-2)^2 + (-3)^2} \approx 3.60555$

Calculating the Modulus of $2$:

Learn how to calculate the modulus of the complex number $2$ step by step:

  1. Calculate the square of the real part (2): $2^2 = 4$
  2. Take the square root of the sum: $\sqrt{4} = 2$

The modulus of $2$ is $2$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{2^2} = 2$

Calculating the Modulus of $2i$:

Learn how to calculate the modulus of the complex number $2i$ step by step:

  1. Calculate the square of the imaginary part (2): $2^2 = 4$
  2. Take the square root of the sum: $\sqrt{4} = 2$

The modulus of $2i$ is $2$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{2^2} = 2$

Calculating the Modulus of $-3i$:

Learn how to calculate the modulus of the complex number $-3i$ step by step:

  1. Calculate the square of the imaginary part (-3): $(-3)^2 = 9$
  2. Take the square root of the sum: $\sqrt{9} = 3$

The modulus of $-3i$ is $3$.

Reminder: Do not include “i” when calculating moduli.

Modulus calculation: $\sqrt{(-3)^2} = 3$

Posted on

HOW TO PLOT COMPLEX NUMBERS STEP BY STEP

This page demonstrates how to graph complex numbers on a coordinate plane, with the horizontal axis representing real numbers and the vertical axis representing imaginary numbers. We’re plotting several points: 3 + 2i, -4 + 5i, -2 – 3i, 6 – 1i, 0 + 4i, -7 + 0i, and 0 + 0i. Each point is shown by moving along the axes based on its real and imaginary components, and then marking its position on the graph.

Detailed Explanations:

For the complex number $3 + 2i$:

Move 3 units along the real axis (x-axis).

Move 2 units along the positive imaginary axis (y-axis).

Mark a point at the resulting position.

For the complex number $-4 + 5i$:

Move 4 units to the left along the real axis (x-axis).

Move 5 units along the positive imaginary axis (y-axis).

Mark a point at the resulting position.

For the complex number $-2 – 3i$:

Move 2 units to the left along the real axis (x-axis).

Move 3 units down along the negative imaginary axis (y-axis).

Mark a point at the resulting position.

For the complex number $6 – 1i$:

Move 6 units to the right along the real axis (x-axis).

Move 1 unit down along the negative imaginary axis (y-axis).

Mark a point at the resulting position.

For the complex number $0 + 4i$:

Move 4 units along the positive imaginary axis (y-axis).

Mark a point at the resulting position on the positive imaginary axis.

For the complex number $-7 + 0i$:

Move 7 units to the left along the real axis (x-axis).

Mark a point at the resulting position on the negative real axis.

For the complex number $0 + 0i$:

Place a point at the origin (0, 0).

Posted on

Operations with roots of negative numbers

Our page provides a comprehensive guide to understanding and calculating the square roots of negative numbers, a fundamental concept in the study of complex and imaginary numbers. We start with the simple task of finding the square root (√) of -4, breaking down the number and applying the property of square roots to simplify the calculation. The result, 2i, is obtained by evaluating each square root separately. We then extend this method to calculate the product and sum of the square roots of two negative numbers, -4 and -9, and -4 and -16, respectively. Each example is broken down into clear steps, with explanations to aid understanding. The aim is to help learners understand how to perform these calculations efficiently and accurately. We also delve into the concept of i squared (i²), which is a key component in these calculations.

Calculating the Square Root of Negative Numbers

In this example, we will calculate the square root of -4. Understanding the square root of negative numbers is a fundamental concept in complex numbers and imaginary numbers.

Step 1: Break Down the Number

Recognize that -4 can be written as -1 times 4:

\(-4 = -1 \times 4\)

Step 2: Apply the Property of Square Roots

Apply the property of square roots that says the square root of a product is the product of the square roots:

\(\sqrt{-4} = \sqrt{-1 \times 4} = \sqrt{-1} \times \sqrt{4}\)

Step 3: Evaluate Each Square Root

Evaluate each square root separately. The square root of -1 is \(i\), and the square root of 4 is 2:

\(\sqrt{-1} \times \sqrt{4} = i \times 2 = 2i\)

Conclusion

So, the square root of -4 is \(2i\). This is a basic example of how to calculate the square root of a negative number.

Efficient Calculation

The calculation can be written in one efficient line as follows:

\(\sqrt{-4} = \sqrt{-1 \times 4} = \sqrt{-1} \times \sqrt{4} = i \times 2 = 2i\)

Calculating the Product of Square Roots of Negative Numbers

In this example, we will calculate the product of the square roots of -4 and -9. Understanding the square roots of negative numbers is a fundamental concept in complex numbers and imaginary numbers.

Step 1: Break Down the Numbers

Recognize that -4 can be written as -1 times 4 and -9 can be written as -1 times 9:

\(-4 = -1 \times 4, -9 = -1 \times 9\)

Step 2: Apply the Property of Square Roots

Apply the property of square roots that says the square root of a product is the product of the square roots:

\(\sqrt{-4} \times \sqrt{-9} = \sqrt{-1 \times 4} \times \sqrt{-1 \times 9} = \sqrt{-1} \times \sqrt{4} \times \sqrt{-1} \times \sqrt{9}\)

Step 3: Evaluate Each Square Root

Evaluate each square root separately. The square root of -1 is \(i\), the square root of 4 is 2, and the square root of 9 is 3:

\(\sqrt{-1} \times \sqrt{4} \times \sqrt{-1} \times \sqrt{9} = i \times 2 \times i \times 3\)

Step 4: Evaluate \(i \times i\)

Remember that \(i \times i = i^2\), which is equal to -1:

\(i \times 2 \times i \times 3 = i^2 \times 2 \times 3 = -1 \times 2 \times 3 = -6\)

Conclusion

So, the product of the square roots of -4 and -9 is \(-6\). This is a basic example of how to calculate the product of the square roots of negative numbers.

Efficient Calculation

The calculation can be written in one efficient line as follows:

\(\sqrt{-4} \times \sqrt{-9} = \sqrt{-1 \times 4} \times \sqrt{-1 \times 9} = \sqrt{-1} \times \sqrt{4} \times \sqrt{-1} \times \sqrt{9} = i \times 2 \times i \times 3 = i^2 \times 2 \times 3 = -1 \times 2 \times 3 = -6\)

Calculating the Sum of Square Roots of Negative Numbers

In this example, we will calculate the sum of the square roots of -4 and -16. Understanding the square roots of negative numbers is a fundamental concept in complex numbers and imaginary numbers.

Step 1: Break Down the Numbers

Recognize that -4 can be written as -1 times 4 and -16 can be written as -1 times 16:

\(-4 = -1 \times 4, -16 = -1 \times 16\)

Step 2: Apply the Property of Square Roots

Apply the property of square roots that says the square root of a product is the product of the square roots:

\(\sqrt{-4} + \sqrt{-16} = \sqrt{-1 \times 4} + \sqrt{-1 \times 16} = \sqrt{-1} \times \sqrt{4} + \sqrt{-1} \times \sqrt{16}\)

Step 3: Evaluate Each Square Root

Evaluate each square root separately. The square root of -1 is \(i\), the square root of 4 is 2, and the square root of 16 is 4:

\(\sqrt{-1} \times \sqrt{4} + \sqrt{-1} \times \sqrt{16} = i \times 2 + i \times 4\)

Step 4: Factor Out the Common Factor

Factor out the common factor \(i\):

\(i \times 2 + i \times 4 = i \times (2 + 4) = i \times 6 = 6i\)

Conclusion

So, the sum of the square roots of -4 and -16 is \(6i\). This is a basic example of how to calculate the sum of the square roots of negative numbers.

Efficient Calculation

The calculation can be written in one efficient line as follows:

\(\sqrt{-4} + \sqrt{-16} = \sqrt{-1 \times 4} + \sqrt{-1 \times 16} = \sqrt{-1} \times \sqrt{4} + \sqrt{-1} \times \sqrt{16} = i \times 2 + i \times 4 = i \times (2 + 4) = i \times 6 = 6i\)

Posted on

Complex Number Division Examples Step by Step

Our page provides step-by-step examples of complex number division, ranging from simple to advanced scenarios. We begin with a straightforward example of dividing by the imaginary unit ‘i’, explaining the technique of multiplying the numerator and denominator by ‘i’ to eliminate it from the denominator. The next example demonstrates how to divide the imaginary unit ‘i’ by a complex number, using the conjugate of the denominator to simplify the process. The final example extends this method to dividing one complex number by another. Each example is broken down into clear steps, with explanations to aid understanding. The aim is to help learners understand how to divide complex numbers and express them in the standard form a + bi.

Complex Number Division Examples

Example 1: Dividing by \( i \): \( \frac{1}{i} \)

When dividing by \( i \), we want to eliminate the imaginary unit from the denominator. This can be achieved by multiplying the numerator and denominator by \( i \):

\[ \frac{1}{i} \times \frac{i}{i} = \frac{i}{i^2} \]

Here, we multiplied the numerator and denominator by \( i \) to get rid of \( i \) in the denominator. This is a common technique used when dividing by complex numbers.

Next, we simplify the denominator. Remember that \( i^2 = -1 \), so we can replace \( i^2 \) with \( -1 \) in the denominator:

\[ \frac{i}{-1} \]

Finally, dividing \( i \) by \( -1 \) gives us the result in standard form:

\[ -i \]

Example 2: Dividing \( i \) by a complex number: \( \frac{i}{1+i} \)

Here, we multiply the numerator and denominator by the conjugate of the denominator, \( 1-i \), to eliminate the imaginary part from the denominator:

Step 1: Multiply the numerator and denominator by the conjugate of the denominator: \( \frac{i}{1+i} \times \frac{1-i}{1-i} \)
Step 2: Simplify the numerator: \( i \times (1-i) = i – i^2 = i + 1 \)
Step 3: Simplify the denominator: \( (1+i)(1-i) = 1^2 – i^2 = 1 – (-1) = 2 \)
Step 4: Divide both the real and imaginary parts of the numerator by the denominator: \( \frac{i+1}{2} = \frac{1}{2} + \frac{1}{2}i \)

Example 3: Dividing a complex number by another complex number: \( \frac{1+2i}{3+4i} \)

Here, we multiply the numerator and denominator by the conjugate of the denominator, \( 3-4i \), to eliminate the imaginary part from the denominator:

Step 1: Multiply the numerator and denominator by the conjugate of the denominator: \( \frac{1+2i}{3+4i} \times \frac{3-4i}{3-4i} \)
Step 2: Simplify the numerator: \( (1+2i) \times (3-4i) = 3 + 6i – 4i – 8i^2 = 3 + 2i + 8 = 11 + 2i \)
Step 3: Simplify the denominator: \( (3+4i) \times (3-4i) = 9 – 16i^2 = 9 + 16 = 25 \)
Step 4: Divide both the real and imaginary parts of the numerator by the denominator: \( \frac{11+2i}{25} = \frac{11}{25} + \frac{2}{25}i \)

Dividing Complex Numbers:

Let’s break down the process of dividing a complex number \(a+bi\) by another complex number \(c+di\):

Step 1: Multiply by the conjugate of the denominator

The goal here is to eliminate the imaginary part from the denominator. We can do this by multiplying both the numerator and the denominator by the conjugate of the denominator. The conjugate of \(c+di\) is \(c-di\).

So, we have:

\[ \frac{a+bi}{c+di} \times \frac{c-di}{c-di} \]

Step 2: Simplify the numerator

We distribute the multiplication across the terms in the numerator:

\[ (a+bi) \times (c-di) = ac – adi + bci – bdi^2 \]

Remember that \(i^2 = -1\), so we can simplify this to:

\[ ac – adi + bci + bd = (ac+bd) + (bc-ad)i \]

Step 3: Simplify the denominator

We distribute the multiplication across the terms in the denominator:

\[ (c+di) \times (c-di) = c^2 – cdi + cdi – d^2i^2 \]

The \(cdi\) and \(-cdi\) terms cancel out, and \(i^2 = -1\), so we can simplify this to:

\[ c^2 + d^2 \]

Step 4: Divide both the real and imaginary parts of the numerator by the denominator

We divide the real part \(ac+bd\) and the imaginary part \(bc-ad\) by the denominator \(c^2 + d^2\):

\[ \frac{(ac+bd) + (bc-ad)i}{c^2 + d^2} = \frac{ac+bd}{c^2 + d^2} + \frac{bc-ad}{c^2 + d^2}i \]

This is the final result in standard form. Each step of the process is explained in detail, and the reason for each step is provided. This should help make the process of dividing by a complex number clearer.

Why was the math book sad? Because it had too many problems, and some of them were complex!
Posted on

Complex Number Multiplication Quiz

Example 1: (2+3i)(1+2i)

First: Multiply the real parts: 2 × 1 = 2

Outer: Multiply the real part of the first number with the imaginary part of the second number: 2 × 2i = 4i

Inner: Multiply the imaginary part of the first number with the real part of the second number: 3i × 1 = 3i

Last: Multiply the imaginary parts: 3i × 2i = 6i². Remember, i² = -1, so 6i² = -6.

Combining the results: 2 + 4i + 3i – 6 = -4 + 7i

Example 2: (1-i)(2+3i)

First: Multiply the real parts: 1 × 2 = 2

Outer: Multiply the real part of the first number with the imaginary part of the second number: 1 × 3i = 3i

Inner: Multiply the imaginary part of the first number with the real part of the second number: -i × 2 = -2i

Last: Multiply the imaginary parts: -i × 3i = -3i². Remember, i² = -1, so -3i² = 3.

Combining the results: 2 + 3i – 2i + 3 = 5 + i

Example 3: (4-2i)(-1+i)

First: Multiply the real parts: 4 × -1 = -4

Outer: Multiply the real part of the first number with the imaginary part of the second number: 4 × i = 4i

Inner: Multiply the imaginary part of the first number with the real part of the second number: -2i × -1 = 2i

Last: Multiply the imaginary parts: -2i × i = -2i². Remember, i² = -1, so -2i² = 2.

Combining the results: -4 + 4i + 2i + 2 = -2 + 6i

Now, let’s practice with the quiz below!

Practice Quiz

Sample Answer Formats: (1+2i), (-3-4i), 0+4i, 5, -2i, 2+0i, -3, 0-5i, 4i, -6

Posted on

Complex Number Addition Quiz

Complex Number Addition Quiz

Complex Number Addition Quiz

Welcome to our interactive Complex Number Addition Quiz! Designed to enhance your mathematical skills, this quiz offers a hands-on approach to understanding and mastering the art of adding complex numbers. Whether you’re a student looking to practice, a teacher sourcing materials, or just someone keen on refreshing their math knowledge, this tool is perfect for you.

Complex numbers, comprising both real and imaginary parts, play a crucial role in advanced mathematics, engineering, and physics. By practicing with our quiz, you’ll not only improve your proficiency in handling complex numbers but also strengthen your foundational math skills. Remember to always include the real part in your answer, even if it’s 0. Dive in and challenge yourself!

Complex Number Addition Quiz

Directions: Simplify your answer before inputting it. Always include the real part, even if it’s 0. For example, for the sum “5+2i+6-2i”, input “11+0i” (not just “11”).

Sample Answer Format: 1+2i, -3-4i, 0+4i

Posted on

Complex Number Operations: A Reference Guide

Complex Number Operations: A Reference Guide

This reference guide provides a concise overview of the fundamental operations involving complex numbers, essential for students, educators, and math enthusiasts.

Key Operations and Concepts

1. Representation: A complex number is denoted as \(a + bi\), where \(a\) is the real part, \(b\) is the imaginary part, and \(i\) is the square root of -1.

Example: The number \(3 + 4i\) has a real part of 3 and an imaginary part of 4.

2. Addition:

\((a + bi) + (c + di) = (a + c) + (b + d)i\)

3. Subtraction:

\((a + bi) – (c + di) = (a – c) + (b – d)i\)

4. Multiplication:

\((a + bi) \times (c + di) = (ac – bd) + (ad + bc)i\)

5. Division:

\(\frac{a + bi}{c + di} = \frac{(a + bi) \times (c – di)}{c^2 + d^2}\)

6. Conjugate: The conjugate of \(a + bi\) is \(a – bi\).

7. Modulus: The modulus of a complex number \(a + bi\) is:

\(|a + bi| = \sqrt{a^2 + b^2}\)

8. Argument: The argument of a complex number is the angle it forms with the positive x-axis in the complex plane.

9. Polar Form: A complex number can be represented in polar form as:

\(r(\cos(\theta) + i\sin(\theta))\), where \( r \) is the modulus and \( \theta \) is the argument.

10. Euler’s Formula:

\(e^{i\theta} = \cos(\theta) + i\sin(\theta)\)

For more in-depth explanations and applications of complex numbers, consider exploring advanced mathematical resources or courses.